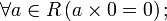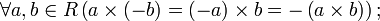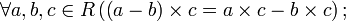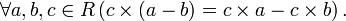Кольцо (алгебра)

Кольцо - это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел.

Определения

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:

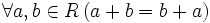1. $\forall a, b \in R \left(a + b = b + a\right)$ — коммутативность сложения;
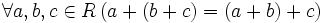2. $\forall a, b, c \in R \left(a + (b + c) = (a + b) + c\right)$ — ассоциативность сложения;
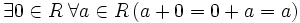3. $\exists 0 \in R\; \forall a \in R \left(a + 0 = 0 + a = a\right)$ — существование нейтрального элемента относительно сложения;
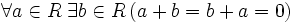4. $\forall a \in R\; \exists b \in R \left(a + b = b + a = 0\right)$ — существование обратного элемента относительно сложения;
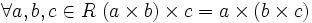5. $\forall a, b, c \in R\; (a \times b) \times c=a \times (b \times c)$ — ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы)
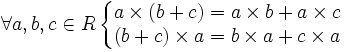6. $\forall a, b, c \in R \left\{\begin{matrix} a \times (b + c) = a \times b + a \times c \\ (b + c) \times a = b \times a + c \times a \end{matrix}\right.$ — дистрибутивность.

Иными словами, кольцо — это универсальная алгебра 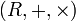$\left(R, +, \times \right)$, такая что алгебра 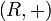$\left(R, + \right)$ — абелева группа, алгебра 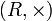$\left(R, \times \right)$ — полугруппа и операция + дистрибутивна относительно $\times$.

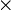Ассоциативные кольца могут обладать следующими дополнительными свойствами:

• наличие единицы: 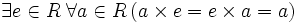$\exists e \in R\; \forall a \in R \left(a \times e = e \times a = a\right)$ (кольцо с единицей);
• коммутативность умножения: 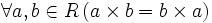$\forall a, b \in R \left(a \times b = b \times a\right)$ (коммутативное кольцо);
• отсутствие делителей нуля: $\forall a, b \in R \left(a \times b = 0 \Rightarrow a = 0 \or b = 0\right)$.

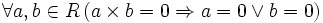Кольца, для которых выполнены все вышеперечисленные условия, называются целостными (иногда также областями целостности или просто областями, хотя условие коммутативности не всегда считается обязательным).

Иногда под ассоциативным кольцом понимают ассоциативное кольцо с единицей. Но имеются примеры ассоциативных колец без единицы, например — нулевое кольцо, кольцо чётных чисел, или же любой несобственный идеал в кольце. Рассматриваются также неассоциативные кольца без единицы, например лиевские кольца и др.

Связанные определения

• Подмножество 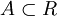$A\subset R$ назывется подкольцом R, если A само является кольцом относительно операций, определенных в R. По определению, оно непусто, поскольку содержит нулевой элемент.
• Ассоциативное кольцо с единицей 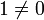$1 \neq 0$, в котором каждый ненулевой элемент обратим, называется телом.
• Коммутативное тело называется полем.

Простейшие свойства

Пусть R — кольцо, тогда выполнены следующие свойства:

1. $\forall a \in R \left(a \times 0 = 0 \right);$
2. $\forall a, b \in R \left(a \times \left( -b \right) = \left( -a \right) \times b = - \left( a \times b \right) \right);$
3. $\forall a, b, c \in R \left(\left(a - b \right) \times c = a\times c - b\times c \right);$
4. $\forall a, b, c \in R \left(c \times \left(a - b \right) = c\times a - c\times b \right).$

Примеры

• {0} — тривиальное кольцо, состоящее из одного нуля. Это единственное кольцо, в котором ноль является мультипликативной единицей.
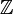• $\mathbb{Z}$ — целые числа (с обычным сложением и умножением).
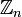• $\mathbb{Z}_n$ — кольцо вычетов по модулю натурального числа n.
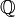• $\mathbb{Q}$ — кольцо рациональных чисел, являющееся полем.
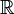• $\mathbb{R}$ — кольцо вещественных чисел, являющееся полем.
• $\mathbb{R}[x_1,x_2,...,x_n]$ — кольцо многочленов от n переменных над полем $\mathbb{R}$.
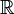• Кольцо алгебраических целых чисел.
• $\Z[i]$ — кольцо гауссовых целых чисел.
• Кольцо когомологий.

См. также

• Алгебра над кольцом
• Бимодуль над кольцом
• Идеал
• Модуль над кольцом

• Артиново кольцо
• Дистрибутивное кольцо
• Евклидово кольцо
• Кольцо Безу
• Кольцо главных идеалов
• Локальное кольцо
• Нётерово кольцо
• Первичное кольцо
• Полулокальное кольцо
• Полупервичное кольцо
• Полупростое кольцо
• Полуцепное кольцо
• Простое кольцо
• Ассоциативное кольцо
• Кольца близкие к ассоциативным
• Цепное кольцо

• Дифференциальное кольцо

• Алгебраическая система

Ссылки

• Винберг Э. Б. Курс алгебры. М.: издательство «Факториал Пресс», 2002, ISBN 5-88688-060-7.
• Бельский А., Садовский Л. Кольца. Квант № 2, 1974.
• Кольцо алгебраическое в Большой советской энциклопедии.