- Матожидание
-
Математи́ческое ожида́ние — понятие среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через
![\mathbb{E}[X]](/pictures/wiki/files/50/27f660bfd70f4a5d381949da7bcc5a85.png) , в русской M[X]. В статистике часто используют обозначение μ.
, в русской M[X]. В статистике часто используют обозначение μ.Содержание
Определение
Пусть задано вероятностное пространство
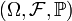 и определённая на нём случайная величина X. То есть, по определению,
и определённая на нём случайная величина X. То есть, по определению, 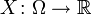 — измеримая функция. Тогда, если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним значением и обозначается
— измеримая функция. Тогда, если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним значением и обозначается 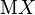 .
.Основные формулы для математического ожидания
- Если FX(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:
![M[X]=\int\limits_{-\infty}^{\infty}\!x\, dF_X(x)](/pictures/wiki/files/53/5e8cb1957b107d0168e265509f991930.png) .
.
Математическое ожидание дискретного распределения
- Если X — дискретная случайная величина, имеющая распределение
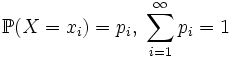 ,
,
то прямо из определения интеграла Лебега следует, что
![M[X]=\sum\limits_{i=1}^{\infty} x_i\, p_i](/pictures/wiki/files/48/046514f2235b8d5afdcb63c95f1f9e47.png) .
.
Математическое ожидание целочисленной величины
- Если X — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
то её математическое ожидание может быть выражено через производящую функцию последовательности {pi}
как значение первой производной в единице: M[X] = P'(1). Если математическое ожидание X бесконечно, то
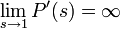 и мы будем писать
и мы будем писать ![P'(1)=M[X]=\infty](/pictures/wiki/files/48/003627519f94cc2f90a364bfd47f2f90.png)
Теперь возьмём производящую функцию Q(s) последовательности «хвостов» распределения {qk}
Эта производящая функция связана с определённой ранее функцией P(s) свойством:
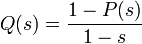 при | s | < 1. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
при | s | < 1. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:- M[X] = P'(1) = Q(1)
Математическое ожидание абсолютно непрерывного распределения
- Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью fX(x), равно
![M[X]=\int\limits_{-\infty}^{\infty}\! x f_X(x)\, dx](/pictures/wiki/files/99/c49316db770d0f068883708a5019088c.png) .
.
Математическое ожидание случайного вектора
Пусть
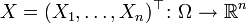 — случайный вектор. Тогда по определению
— случайный вектор. Тогда по определению![M[X]=(M[X_1],\dots,M[X_n])^{\top}](/pictures/wiki/files/56/8b3fdfd5e52b85f96add51e9e6678f69.png) ,
,
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины
Пусть
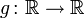 — борелевская функция, такая что случайная величина Y = g(X) имеет конечное математическое ожидание. Тогда для него справедлива формула:
— борелевская функция, такая что случайная величина Y = g(X) имеет конечное математическое ожидание. Тогда для него справедлива формула:![M\left[g(X)\right] = \sum\limits_{i=1}^{\infty} g(x_i) p_i](/pictures/wiki/files/55/7d6e344567887d08e2976bf9b3128104.png) ,
,
если X имеет дискретное распределение;
![M\left[g(X)\right] = \int\limits_{-\infty}^{\infty}\!g(x) f_X(x)\, dx](/pictures/wiki/files/48/02fbac556ec78f173ab79c2955e7ee65.png) ,
,
если X имеет абсолютно непрерывное распределение.
Если распределение
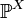 случайной величины X общего вида, то
случайной величины X общего вида, то![M\left[g(X)\right] = \int\limits_{-\infty}^{\infty}\!g(x)\, \mathbb{P}^X(dx)](/pictures/wiki/files/56/819a6e6d7abac1d518b85c8080a9b66c.png) .
.
В специальном случае, когда g(X) = Xk, Математическое ожидание
![M\left[g(X)\right]=M[X^k]](/pictures/wiki/files/48/0ed325d42e4b7001fdb2aff6c41f9ba6.png) называется k-тым моментом случайной величины.
называется k-тым моментом случайной величины.Простейшие свойства математического ожидания
- Математическое ожидание линейно, то есть
-
- M[aX + bY] = aM[X] + bM[Y],
- где X,Y — случайные величины с конечным математическим ожиданием, а
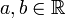 — произвольные константы;
— произвольные константы;
- Математическое ожидание сохраняет неравенства, то есть если
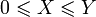 почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того
почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того
-
![0 \leqslant M[X] \leqslant M[Y]](/pictures/wiki/files/101/e67438b55d345e5692ea76871582d31e.png) ;
;
- Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если X = Y почти наверное, то
-
- M[X] = M[Y].
- Математическое ожидание произведения двух независимых случайных величин X,Y равно произведению их математических ожиданий
-
- M[XY] = M[X]M[Y].
Дополнительные свойства математического ожидания
- Неравенство Маркова;
- Теорема Леви о монотонной сходимости;
- Теорема Лебега о мажорируемой сходимости;
- Лемма Фату.
- Математическое ожидание случайной величины X может быть выражено через её производящую функцию моментов G(u) как значение первой производной в нуле: M[X] = G'(0)
Примеры
- Пусть случайная величина имеет дискретное равномерное распределение, то есть
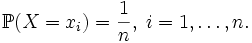 Тогда её математическое ожидание
Тогда её математическое ожидание
равно среднему арифметическому всех принимаемых значений.
- Пусть случайная величина имеет непрерывное равномерное распределение на интервале [a,b], где a < b. Тогда её плотность имеет вид
![f_X(x) = \frac{1}{b-a} \mathbf{1}_{[a,b]}(x)](/pictures/wiki/files/53/55af3f166a3c4dbb6ca304c8662de4ef.png) и математическое ожидание равно
и математическое ожидание равно
![M[X] = \int\limits_{a}^b\!\frac{x}{b-a}\, dx = \frac{a+b}{2}](/pictures/wiki/files/99/caed74b073b2321d979f091640d4c62c.png) .
.
- Пусть случайная величина X имеет стандартное распределение Коши. Тогда
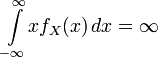 ,
,
то есть математическое ожидание X не определено.
См. также
- Дисперсия случайной величины;
- Моменты случайной величины;
- Условное математическое ожидание;
- Выборочное среднее.
Литература
- В.Феллер Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Под ред. Е. Б. Дынкина. — 2-е изд. — М.: Мир, 1964. — С. 270—272.
Wikimedia Foundation. 2010.

![M[X]=\int\limits_{\Omega}\! X(\omega)\, \mathbb{P}(d\omega).](/pictures/wiki/files/98/b20b2ed0ab35c1f3dd1bad9223e0a76a.png)
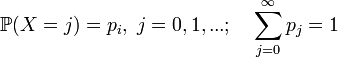
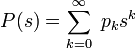
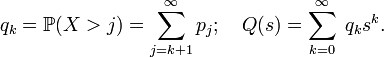
![M[X] = \frac{1}{n} \sum\limits_{i=1}^n x_i](/pictures/wiki/files/57/9e649d3c8a697a90e8a6113971bbb002.png)