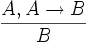- Предикатная логика
-
Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций, и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка.
Содержание
Основные определения
Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов
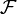 и множества предикатных символов
и множества предикатных символов 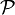 . С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того используются следующие дополнительные символы
. С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того используются следующие дополнительные символы- Символы переменных (обычно x,y,z,x1,y1,z1,x2,y2,z2, и т. д.),
- Пропозициональные связки:
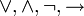 ,
, - Кванторы: всеобщности
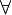 и существования
и существования 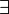 ,
, - Служебные символы: скобки и запятая.
Перечисленные символы вместе с символами из
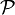 и
и 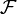 образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:
образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:- Терм есть символ переменной, либо имеет вид
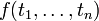 , где f — функциональный символ арности n, а
, где f — функциональный символ арности n, а 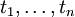 — термы.
— термы. - Атом имеет вид
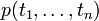 , где p — предикатный символ арности n, а
, где p — предикатный символ арности n, а 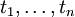 — термы.
— термы. - Формула — это либо атом, либо одна из следующих конструкций:
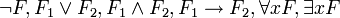 , где F,F1,F2 — формулы, а x — переменная.
, где F,F1,F2 — формулы, а x — переменная.
Переменная x называется связанной в формуле F, если F имеет вид
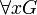 либо
либо 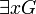 , или же представима в одной из форм
, или же представима в одной из форм 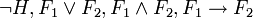 , причем x уже связанна в H, F1 и F2. Если x не связанна в F, ее называют свободной в F. Формулу без свободных переменных называют замкнутой формулой, или предложением. Теорией первого порядка называют любое множество предложений.
, причем x уже связанна в H, F1 и F2. Если x не связанна в F, ее называют свободной в F. Формулу без свободных переменных называют замкнутой формулой, или предложением. Теорией первого порядка называют любое множество предложений.Аксиоматика и доказательство формул
Система логических аксиом логики первого порядка состоит из аксиом исчисления высказываний дополненной двумя новыми аксиомами:
![\forall x A \to A[t/x]](/pictures/wiki/files/48/057a6762519a2b37d5d20d6e50534fd4.png) ,
,![A[t/x] \to \exists x A](/pictures/wiki/files/48/0b266639c5cb3d272730b72242a30d00.png) ,
,
где A[t / x] — формула, полученная в результате подстановки терма t вместо переменной x в формуле A.
Правил вывода 3:
Интерпретация
В классическом случае интерпретация формул логики первого порядка задается на модели первого порядка, которая определяется следующими данными
- Несущее множество
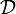 ,
, - Семантическая функция σ, отображающая
- каждый n-арный функциональный символ f из
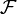 в n-арную функцию
в n-арную функцию  ,
, - каждый n-арный предикатный символ p из
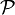 в n-арное отношение
в n-арное отношение 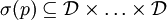 .
.
- каждый n-арный функциональный символ f из
Обычно принято, отождествлять несущее множество
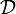 и саму модель, подразумевая неявно семантическую функцию, если это не ведет к неоднозначности.
и саму модель, подразумевая неявно семантическую функцию, если это не ведет к неоднозначности.Предположим s — функция, отображающая каждую переменную в некоторый элемент из
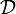 , которую мы будем называть подстановкой. Интерпретация
, которую мы будем называть подстановкой. Интерпретация ![[\![t]\!]_s](/pictures/wiki/files/53/5b43ccd0b69f5bb57eee56c1279a7db6.png) терма t на
терма t на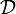 относительно подстановки s задается индуктивно
относительно подстановки s задается индуктивно![[\![x]\!]_s = s(x)](/pictures/wiki/files/101/e23e4a6196a7a91a2e04ed7acb8b4741.png) , если x — переменная,
, если x — переменная,![[\![f(x_1,\ldots,x_n)]\!]_s = \sigma(f)(\![x_1]\!]_s,\ldots,\![x_n]\!]_s)](/pictures/wiki/files/52/4a6b9468ccd62fb8b7bccdd6a8a38e75.png)
В таком же духе определяется отношение истинности
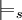 формул на
формул на 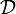 относительно s
относительно s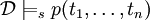 , тогда и только тогда, когда
, тогда и только тогда, когда ![\sigma(p)( \![x_1]\!]_s,\ldots,\![x_n]\!]_s)](/pictures/wiki/files/53/5d456756ab61ee475274d95dc3e5cac0.png) ,
,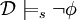 , тогда и только тогда, когда
, тогда и только тогда, когда 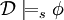 — ложно,
— ложно,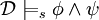 , тогда и только тогда, когда
, тогда и только тогда, когда 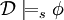 и
и 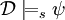 истинны,'
истинны,'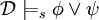 , тогда и только тогда, когда
, тогда и только тогда, когда 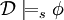 или
или 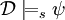 истинно,
истинно,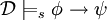 , тогда и только тогда, когда
, тогда и только тогда, когда 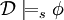 влечет
влечет 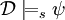 ,
,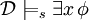 , тогда и только тогда, когда
, тогда и только тогда, когда 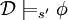 для некоторой подстановки s', которая отличается от s только на переменной x,
для некоторой подстановки s', которая отличается от s только на переменной x,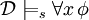 , тогда и только тогда, когда
, тогда и только тогда, когда 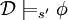 для всех подстановок s', которые отличается от s только на переменной x.
для всех подстановок s', которые отличается от s только на переменной x.
Формула φ, истинна на
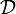 , что обозначается как
, что обозначается как 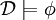 , если
, если 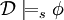 , для всех подстановок s. Формула φ называется общезначимой, что обозначается как
, для всех подстановок s. Формула φ называется общезначимой, что обозначается как 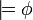 , если
, если 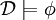 для всех моделей
для всех моделей 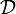 . Формула φ называется выполнимой , если
. Формула φ называется выполнимой , если 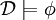 хотябы для одной
хотябы для одной 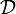 .
.Свойства и основные результаты
Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являются полнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). При этом если непротиворечивость более или менее очевидна, то полнота — нетривиальный результат полученный Гёделем в 1930 году (теорема Гёделя о полноте). По сути теорема Гёделя устанавливает фундаментальную эквивалентность понятий доказуемости и общезначимости.
Логика первого порядка обладает свойством компактности: если некоторое множество формул не выполнимо, то невыполнимо также некоторое его конечное подмножество.
Согласно теореме Левенгейма — Сколема если множество формул имеет модель, то оно также имеет модель не более чем счетной мощности. С этой теоремой связан парадокс Сколема, который однако является лишь мнимым парадоксом.
Использование
Логика первого порядка как формальная модель рассуждений
Являясь формализованым аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности. Рассмотрим классический пример формализации утверждений естественного языка в логике первого порядка.
Возьмем рассуждение «Каждый человек смертен. Конфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» через ЧЕЛОВЕК(x) и «x смертен» через СМЕРТЕН(x). Тогда утверждение «каждый человек смертен» может быть представлено формулой:
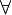 x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой
x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой( 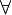 x(ЧЕЛОВЕК(x) → СМЕРТЕН(x))
x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) 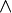 ЧЕЛОВЕК(Конфуций) ) → СМЕРТЕН(Конфуций)
ЧЕЛОВЕК(Конфуций) ) → СМЕРТЕН(Конфуций)Обобщения
Литература
- Гильберт Д., Аккерман В. Основы теоретической логики. М., 1947
- Клини С. К. Введение в метаматематику. М., 1957
- Мендельсон Э. Введение в математическую логику. М., 1976
- Новиков П. С. Элементы математической логики. М., 1959
- Черч А. Введение в математическую логику, т. I. М. 1960
Wikimedia Foundation. 2010.